Area Of A Base - In this section, we will study the base area of a triangular prism with solved examples. The area of the base of a triangular prism is the area of the triangle of the prism. Let's start with the background needed to understand the base area of a triangular prism. Remember that a prism is a solid with equal polygonal ends (bases), parallelograms, and plane sides, and it has the same cross-sectional area along its entire length.
A prism with three faces as a rectangle and two triangles as a base (one triangle as the top) is called a triangular prism. It is a three-sided prism, where the base and the top are equal triangles and the other 3 sides are rectangles. The two triangles are parallel and congruent. The rectangles do not have to match each other.
Area Of A Base

The area of the base of a triangular prism is defined as the total area covered by the bases of a triangular prism. The base area of a triangular prism is expressed in square units. The area of the base of a triangular prism can be calculated using different formulas, depending on the known parameters and the type of triangle at the base. Let us understand these formulas in the following sections.
Question Video: Finding The Length Of A Base In A Trapezoid Given The Other Base's Length, The Height, And The Area
For a triangular prism, if the length of the sides of the triangular base of the prism is given, the area of its base can be obtained as:
Example: How to find the base area of a triangular prism based on the length of the sides of the base triangle: a = 20 units, b = 10 units and c = 20 units?
Base area of the given triangular prism = √[s(s − a)(s − b)(s − c)] = √[25(25 − 20)(25 − 10)(25 − 20)] = √[ 25 (5)(15)(5)] = 25√15 square units.
For a triangular prism, given the length of the base and the height of the base triangle, the area of the base can be obtained as:
Ways To Find Cubic Feet
Example: How to find the area of the base of a triangle prism with height h = 10 units and base b = 20 units?
Solution: Area of the base of the given triangular prism = (1/2) × b × h = (1/2) × 20 × 10 = 100 square units
The base area of a triangular prism is defined as the area or surface covered by the bases of a triangular prism. A triangular prism has 2 triangular bases.
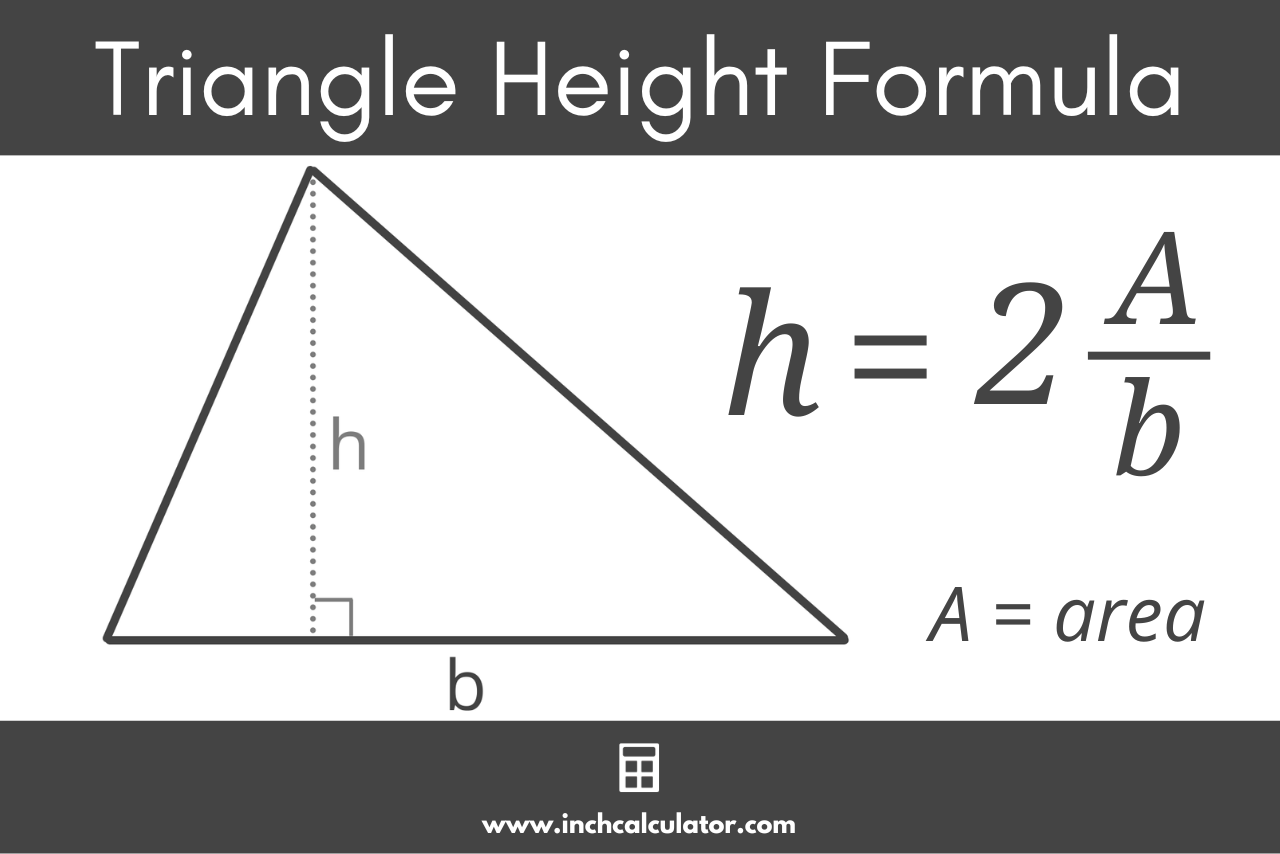
Using the triangle area formula for the type of triangle given in the base, we can calculate and solve for the length of the base by substituting the known values into the formula. The lateral area formula is used to find the lateral surface area of any solid object. The area of each figure is only the area of the non-base faces. Lateral area formulas help calculate the lateral area of a variety of shapes, including cubes, cubes, cylinders, cones, and spheres.
Area Of Trapezoids: Formula, Examples, Derivation
The lateral area formula is different for different types of objects. So there are many side area formulas which are explained below. The side area does not include the base area of the object and also the face parallel to the base. The formula for the lateral area of different objects is given in the table below:
For 3D shapes we measure the lateral area. Below is a detailed list of tables to help you understand the lateral area formula.
Use our free online calculator to solve difficult questions. With this, find solutions in simple and easy steps.
Example 1: The length, width, and height of a cube are 6 units, 2 units, and 16 units, respectively. Calculate the lateral surface area of the cube.
Solved: 'what Is The Base, Perimeter Of Base, And Height Of This Figure? No Links Pls Or I Will Report U! Henuse The Net To Find The Surface = Area 12 Ft
Example 2: The radius of a sphere is 4 units. This sphere is cut into two equal halves. Calculate the lateral area of the two objects using the formula.
Answer: Lateral area of sphere = 201,142 square units and lateral area of hemisphere/curve = 100,571 square units
Example 3: Find the lateral area of the cube using the lateral area formula of 7 units.

The formula for the lateral area of the cone LSA =πrl. where r is the radius of a cone, l is the height of the cone, and π (pi) is a constant term with a value of 3.14 or 7.22.
Solved 1) Determine The Minimum Of The Function Where The
(If the diameter of the sphere = 2r). where r is the radius of a sphere, h is the height of the sphere, and π (pi) is a constant term with a value of 3.14 or 7.22.
The lateral area of the cylinders is expressed as LSA=2πrh. where r is the radius of the circular base of the cylinder, h is the height of the cylinder and π (pi) is a constant term with a value of 3.14 or 7.22.
The lateral area of cuboids is expressed as LSA = 2h (l+b). where l, b and h are the length, width and height of a cube. The area of a right triangle is the part covered by the boundary of the triangle. A right triangle is a triangle in which one of its angles is right (90 degrees). It is simply known as a right triangle. In a right triangle, the side opposite the right angle is called the hypotenuse and the other two sides are called the legs. The two bases can be called base and height interchangeably. The area of the triangle angle formula is given in the figure below.
The area of a right triangle, as we mentioned before, is the space inside. This space is divided into squares of unit length, and the number of square units inside the right triangle is its area. Area is measured in square units. Consider the following right triangle with base 4 units and height 3 units.
Volume And Surface Area Of A Pyramid (8 Examples!)
Can you count the number of unit squares inside this triangle? There are a total of 6 square units. So the area of the upper triangle is 6 square units. But the area of a right triangle cannot always be calculated by counting the number of squares. There must be a formula for this. Let's look at the formula for finding the area of a right triangle.
In the example above, if we multiply the base and the height, we get 3x4 = 12, and if we divide by 2, we get 6. So the area of a right triangle is obtained by multiplying its base and height and then it is obtained. Semi-finished product
Consider a rectangle of length l and width w. Also draw a diagonal. You can see that the rectangle is divided into two right triangles.
We know that the area of a rectangle is length x width. So the area of the above rectangle is l × w. We see that two right triangles are congruent because they can be arranged so that one overlaps the other. Therefore, the area of a rectangle is twice the area of a right triangle. that is significant
Solved 9. Find The Area Of The Figure. D 3 M с 1 14 M A S B
So the formula for the area of a right triangle is area of a right triangle = 1/2 x base x height.
Let's remember the Pythagorean theorem, which states that the square of the hypotenuse in a right triangle is the sum of the squares of the other two sides. that is (hypotenosis)
Although it is not possible to find the area of a right triangle with a hypotenuse, but if we know a base and an altitude along with the hypotenuse, its area is possible. Let's look at an example.
Example: Find the area of a right triangle whose base is 6 inches and whose hypotenuse is 10 inches.
Surface Area Of Prisms, Cylinders, And Pyramids
Therefore, area of the given triangle = 1/2 × base × height = 1/2 × 6 × 8 = 24 inches
The area of a right triangle is the total space or area covered by a right triangle. It is expressed in square units. Some common units used to represent surface area are m
The area of a right triangle with base b and height h is 1/2 x base x height (or) 1/2 x b x h square units.
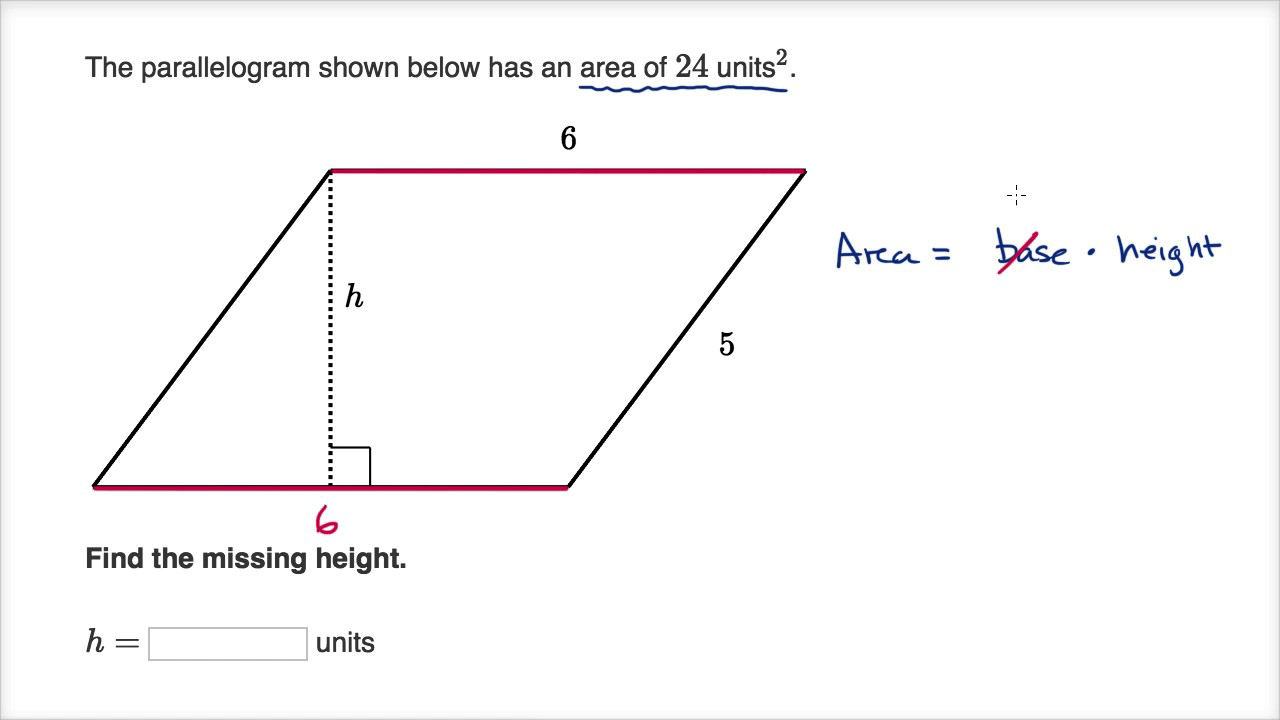
The area of a right triangle with base b and height h is obtained using the formula 1/2 × b × h and its perimeter is obtained by adding all sides. If only two sides are given, we use the Pythagorean theorem to find the third side.
Base Area Of A Triangular Prism
If only the altitude and hypotenuse of a right triangle are given, before finding the area of the triangle, we must find the base using the Pythagorean theorem. We can then use the formula 1/2 x base x height to find its area. For example, to find the area of a right triangle with a height of 4 cm and a hypotenuse of 5 cm, we first find its base using the Pythagorean theorem. then we get
If only the base and hypotenuse of a right triangle are given, before finding the area of the triangle, first
Base area of a square pyramid, surface area of a square base pyramid, area of a circular base, area of a base of a prism, base area of a triangular pyramid, area of base of a rectangular prism, surface area of a cone without base, base area of cone formula, base area of a square, base area of cone, base area of a pyramid, area of a triangle base
0 Comments